Représentation des solutions d'une équation différentielle linéaire d'ordre 1
Représentation des solutions de $\left\{ \begin{array}{rcl} y'-2y&=&\mathrm{e}^t+3\\ y(0)&=&a\end{array}\right.$, où $a$ est un paramètre réel.La solution du problème de Cauchy est $f:t\mapsto \left(\dfrac{5}{2}+a\right)\mathrm{e}^{2t}-\mathrm{e}^t-\dfrac{3}{2}$. Étudions cette fonction.
Déjà, on remarque que $\displaystyle\lim_{t\to -\infty} f(t)=-\dfrac{3}{2}$ . Par ailleurs, la fonction $f$ est dérivable sur $\R$ en tant que somme de fonctions dérivables et $$ \forall t\in\R,\quad f'(t)=(2a+5)\mathrm{e}^{2t}-\mathrm{e}^t. $$ Soit $t\in\R$. On a $$ f'(t)\geq 0 \iff (2a+5)\mathrm{e}^{t}-1\geq 0 \iff (2a+5)\mathrm{e}^{t}\geq 1. $$ Il y a des cas à distinguer pour poursuivre.
- Cas où $a= -\dfrac{5}{2}$. On a alors $2a+5= 0$, donc
$$
f'(t)\geq 0 \iff 0\geq 1
$$
et comme cette dernière assertion n'est jamais vraie, on conclut que $f$ est strictement décroissante.
De plus, $f(t)=-\mathrm{e}^t-\dfrac{3}{2}$, donc $\displaystyle\lim_{t\to +\infty} f(t)=-\infty$. Finalement :
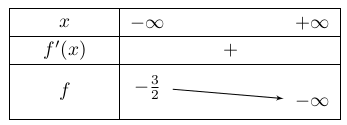
- Cas où $a\lt -\dfrac{5}{2}$. On a alors $2a+5\lt 0$, donc
$$
f'(t)\geq 0 \iff \mathrm{e}^{t}\leq \dfrac{1}{2a+5}
$$
et comme cette dernière assertion n'est jamais vraie, on conclut que $f$ est strictement décroissante.
De plus, $f(t)=\mathrm{e}^{2t}\left( \dfrac{5}{2}+a-\mathrm{e}^{-t}-\dfrac{3}{2}\mathrm{e}^{-2t}\right)$, donc $\displaystyle\lim_{t\to +\infty} f(t)=-\infty$.
Finalement :

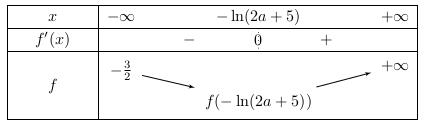
- Cas où $a\gt -\dfrac{5}{2}$. On a alors $2a+5\gt 0$, puis
$$
f'(t)\geq 0 \iff \mathrm{e}^{t}\geq \dfrac{1}{2a+5} \iff t\geq \ln\left(\dfrac{1}{2a+5}\right)\iff t\geq -\ln(2a+5)
$$
De plus, $f(t)=\mathrm{e}^{2t}\left( \dfrac{5}{2}+a-\mathrm{e}^{-t}-\dfrac{3}{2}\mathrm{e}^{-2t}\right)$, donc $\displaystyle\lim_{t\to +\infty} f(t)=+\infty$.
Finalement :